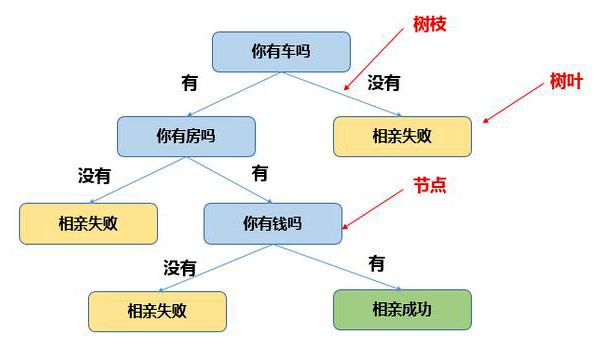
原理解读
决策树(Decision Tree):是在已知各种情况发生概率的基础上,直观运用概率分析的一种图解法。决策树是一种树形结构,其中每个内部节点表示一个属性上的测试,每个分支代表一个测试输出,每个叶节点代表一种类别。由于这种决策分支画成图形很像一棵树的枝干,故称决策树。
核心思想
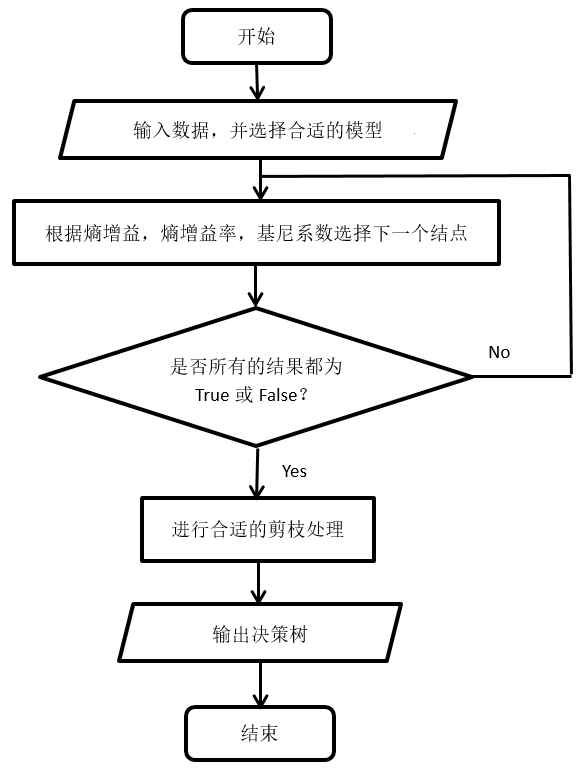
树的构建
- 步骤1:将所有的数据看成是一个节点(根节点),进入步骤2
- 步骤2:根据划分准则,从所有属性中挑选一个对节点进行分割,进入步骤3
- 步骤3:生成若干个子节点,对每一个子节点进行判断,如果满足停止分裂的条件,进入步骤4;否则,进入步骤2
- 步骤4:设置该节点是叶子节点,其输出的结果为该节点数量占比最大的类别
划分准则
信息熵
信息熵:假设样本集合D中第k类样本所占的比例为$p_k(k=1,2,\ldots,y)$,则D的信息熵定义为:
$$Ent(D)=-\displaystyle \sum_{k=1}^y p_klog_2p_k$$
Ent(D)的值越小,则D的纯度越高。
信息增益(ID3)
假设离散属性a有V个不同的取值$\lbrace a^1,a^2,\ldots,a^V \rbrace$,若使用a来对样本集D进行划分,则会产生V个分支节点,其中第v个分支节点包含了D中所有在属性a上取值为$a^v$的样本,记为$D^v$。我们可以计算出$D^v$的信息熵,再给分支结点赋予权重$\frac{\left| D^v \right|}{\left| D \right|}$
则可以计算出用属性a对样本集D进行划分所获得的”信息增益”。
$$Gain(D,a)=Ent(D)-\displaystyle \sum_{v=1}^V \frac{\left| D^v \right|}{\left| D \right|}Ent(D^v)$$
一般而言,信息增益越大,则意味着使用属性a来进行划分所获得的纯度提升越大,ID3决策树学习算法就是以信息增益为准则来划分属性。
增益率(C4.5)
实际上,信息增益准则对可取值数目较多的属性有所偏好,为减少这种偏好可能带来的不利影响,著名的C4.5决策树算法不直接使用信息增益,而是使用”增益率”来选择最优划分属性。
增益率定义为
$$Gain_ratio=\frac{Gain(D,a)}{IV(a)}$$
$$IV(a)=-\displaystyle \sum_{v=1}^V \frac{\left| D^v \right|}{\left| D \right|} log_2 \frac{\left| D^v \right|}{\left| D \right|}$$
需要注意的是,增益率准则对可取值数目较少的属性有所偏好,因此C4.5算法先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
基尼指数(CART)
基尼指数反应了从数据集D中随机抽取两个样本,其类别标记不一致的概率。因此基尼指数越小,则数据集D的纯度越高。
$$Gini(D)=1-\displaystyle \sum_{k=1}^y {p_k}^2$$
属性a的基尼指数定义为
$$Gini_index(D,a)=\displaystyle \sum_{v=1}^V \frac{\left| D^v \right|}{\left| D \right|} Gini(D^v)$$
在选择属性集合时,选择使划分后基尼指数最小的属性作为最优划分属性。
剪枝处理
剪枝(pruning)是决策树学习算法对付”过拟合”的主要手段。
决策树剪枝的基本策略有”预剪枝(prepruning)”和”后剪枝(postpruning)”。
预剪枝(prepruning)
预剪枝:是在决策树生长过程中,对每个结点在划分前先进行估计,若当前结点的划分不能带来决策树泛化性能提升,则停止划分并将当前结点标记为叶子结点。
预剪枝优点:
- 降低过拟合风险
- 显著减少决策树的训练时间开销和测试时间开销
预剪枝缺点: - 因为”贪心”本质,可能带来欠拟合的风险
后剪枝(postpruning)
后剪枝:先从训练集生成一颗完整的决策树,然后自底向上地对非叶结点进行考察,若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升,则将该子树替换为叶节点。
后剪枝优点:
- 泛化性能较好
- 欠拟合风险较小
后剪枝缺点: - 生成完全决策树后进行,并且自底向上对所有非叶结点进行逐一考察,时间开销大
算法流程
代码实战
代码中所用数据为罗斯.昆兰(Ross Quinlan)当年所用的高尔夫模型
其实这里使用的算法并不是ID3,因为老师上课讲错了,误把ID3讲成最小熵,ID3应该是最小熵增益。但是作业要求是实现最小熵的ID3算法,所以我起名为ID3。但是标准的ID3,还需要一个比较的过程,确定哪一种分割是最小熵增益。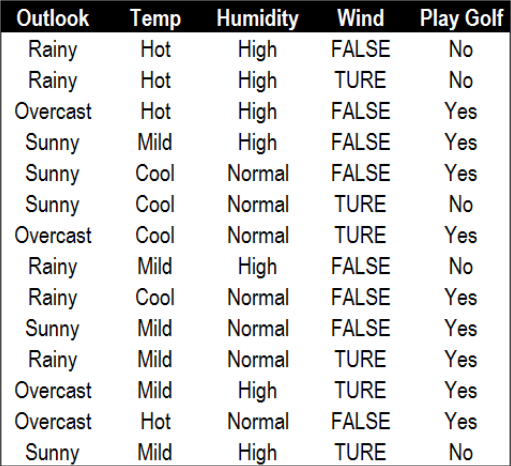
ID3_main.m
1 | %% %获取基本信息 |
ID3_split.m
1 | function bestfeature=ID3_split(data) |
ID3_ent.m
1 | function ent=ID3_ent(data,i) |
ID3_creat.m
1 | function [tree,No]=ID3_creat(data,class_name,tree,No) |
实验结果
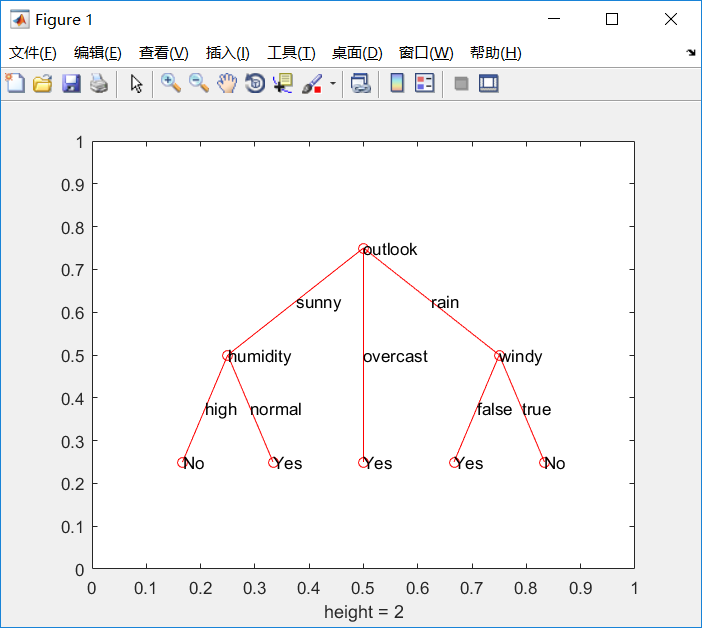
ID3, C4.5, CART性能比较
$$ \begin{array}{|c|c|c|c|c|} 算法 & 结构 & 特征选择 & 连续值 & 缺失值 \ \hline ID3&多叉树&信息增益&不支持&不支持\ C4.5&多叉树&信息增益比&支持&支持\ CART&二叉树&基尼系数&支持&支持\ \end{array}$$
决策树分类优缺点
- 优点:
- 数据量一般不会太大
- 具有很强的可解释性
- 生成的决策树简单直观
- 可以处理多维度输出的分类问题。
- 既可以处理离散值也可以处理连续值
- 可以通过剪枝来权衡欠拟合和过拟合
- 基本不需要预处理,不需要提前归一化,处理缺失值。
- 缺点:
- 树结构受样本影响较大
- 复杂的模型很难用决策树解决
- 寻找最优的决策树是一个NP难的问题
- 如果某些特征的样本比例过大,生成决策树容易偏向于这些特征,这个可以通过调节样本权重来改善